Wachstumsmodelle stammen ursprünglich aus der Biologie, wo sie die direkt beobachtbare Veränderung von Größe oder Gewicht eines Individuums über die Zeit beschreiben. Latente Wachstumsmodelle hingegen modellieren die Veränderung individueller Parameter, die nicht direkt zu beobachten sind (Intelligenz, Lesefähigkeit, Einstellungen …). Charakteristisch für diese Form der Modellierung ist, dass die einzelnen Messungen als fehlerbehaftet angesehen werden, so dass ein direkter Bezug zu den Strukturgleichungsmodellen besteht.
Anders als bei den bisher vorgestellten Modellen wird der Wert der latenten Variablen jedoch nicht als konstant betrachtet. Vielmehr wird davon ausgegangen, dass die individuellen Entwicklungen über die Zeit einer personenspezifischen Wachstumskurve folgen. Die Schätzung eines einfachen Wachstumsmodells erfordert ein Panel mit mindestens drei Wellen; für komplexere Modelle werden zusätzliche Wellen benötigt.
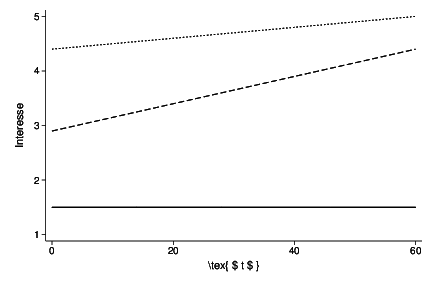
Figure 1: Individuelle Wachstumskurven (idealisiert)
Im Beispiel wird die Zunahme des Interesses am Bundestagswahlkampf während der heißen Phase von Juli bis September 2013 modelliert. Dazu wurden im Rahmen der GLES rund 4000 Wahlberechtigte fünf Mal befragt.
Um zu verstehen wie es möglich ist, nicht nur den aggregierte Anstieg des Interesses am Wahlkampf, sondern auch befragtenspezifische Kurven zu modellieren, muss man sich klarmachen, dass jede Kurve durch zwei Parameter beschrieben werden kann, die dem Achsenabschnitt (Intercept oder kurz I) und der Steigung (slope, S) eines individuellen linearen Regressionsmodells entsprechen. Der Achsenabschnitt erfasst dabei das Ausgangsniveau des Wahlkampfinteresses in der ersten Welle, während die Steigung die tägliche Zunahme des Interesses abbildet.
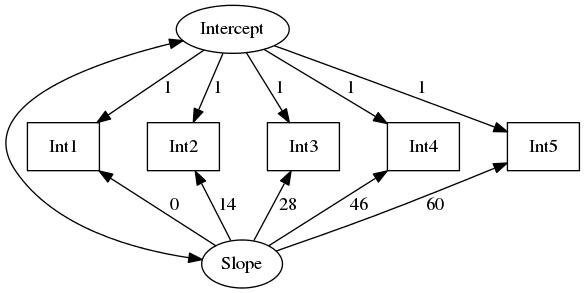
Figure 2: Wachstumsmodell als Strukturgleichungsmodell
Die Abbildung zeigt das zugehörige Strukturgleichungsmodell. Für (fast) alle Pfade sind Restriktionen gesetzt. Diese erklären sich aus der Annahme eines linearen Wachstums. Jeder der fünf Messwerte ist eine Funktion des Achsenabschnitts, der Steigung, und der seit Beginn des Wahlkampfes vergangenen Zeit in Tagen (0, 14, 28, 46, 60). Der einzige Pfad, dessen Koeffizient frei geschätzt wird, ist die Kovarianz zwischen Achsenabschnitt und Steigung. Im Beispiel ist hier ein negativer Wert zu erwarten, da für Personen, die bereits zu Beginn der Kampagne sehr interessiert waren, in der Tendenz eine geringere Zunahme des Interesses, also ein schwächeres “Wachstum” zu erwarten ist. Das Hauptinteresse bei dieser Form der Modellierung gilt jedoch nicht den Pfaden, sondern den personenspezifischen Werten der latenten Variablen sowie deren Mittelwerten.
Latente Wachstumsmodelle in Stata
In Stata läßt sich das Wachstumsmodell in wenigen Zeilen formulieren. Die Anweisungen in Zeile 2 erzeugen die Pfade zwischen dem Achsenabschnitt und den fünf Messwerten und fixieren deren Pfadkoeffizienten auf den Wert von 1. In Zeile 3 werden die entsprechenden Zuweisungen für die lineare Steigung vorgenommen. Von besonderer Bedeutung sind die beiden Optionen in Zeile 4. noconstant unterdrückt die Aufnahme einer zusätzlichen Konstanten in das Meßmodell. Auch die Option means(I S) unterdrückt eine Voreinstellung, nämlich die, dass den latenten Variablen normalerweise ein Mittelwert von 0 zugewiesen wird, was hier offensichtlich nicht zielführend wäre.
use interesse-panel, clear sem (I -> int1@1 int2@1 int3@1 int4@1 int5@1) /// (S -> int1@0 int2@14 int3@28 int4@46 int5@60) /// , noconstant means(I S)
Der erste Teil der umfangreichen Ausgabe spiegelt die Modellstruktur mit ihren zahlreichen Restriktionen wider. Interessanter sind die Informationen zu den latenten Variablen. Das mittlere Interesse zu Beginn des Wahlkampfes lag danach bei 3.08 Punkten, also fast exakt am Mittelpunkt der Skala. Der mittlere Anstieg des Interesses pro Wahlkampftag ist mit 0.0008685 verschwindend gering. Auf die gesamte Dauer von 60 Tagen gerechnet stieg das wahre Interesse am Wahlkampf im Mittel um lediglich 0.052 Skalenpunkte.
Da es sich hier um latente Variablen handelt, werden Achsenabschnitt und Steigung als normalverteilt modelliert. Die entsprechenden Schätzwerte finden sich ganz unten im siebten Feld der Tabelle. Hier zeigt sich, dass die Streuung der Achsenabschnitte (Interesse zu Beginn des Wahlkampfes) recht groß ist. Die Varianz von 0.91 entspricht einer Standardabweichung von .95, d.h. das Interesse streut über den gesamten Wertebereich der Skala. Die geschätzte Varianz der Steigung ist naturgemäß sehr viel kleiner.
Aus dem Mittelwert und der Varianz der Steigung sowie der Annahme einer Normalverteilung der Werte über die Befragten ergibt sich, dass für rund zwei Drittel der Befragten der wahre Wert des Interesses im Laufe des Wahlkampfes (leicht) ansteigt, während er für das verbleibende Drittel (leicht) sinkt.
Latente Wachstumsmodelle in Lisrel (Simplis)
Auch in Lisrel bereitet die Spezifikation des Wachstumsmodell keine besonderen Probleme.
Raw Data From File interesse-panel.lsf Latent Variables: I S Relationships int1 = 1*I + 0 * S int2 = 1*I + 14 * S int3 = 1*I + 28 * S int4 = 1*I + 46 * S int5 = 1*I + 60 * S I = Const S = Const End of Problem
Latente Wachstumsmodelle in MPlus
Dies gilt auch für MPlus. Die eigentliche Modellspezifikation findet sich in der letzten Zeile. Das |-Zeichen signalisiert, daß ein Wachstumsmodell geschätzt werden soll. Links davon finden sich die bereits bekannten latenten Variablen I und S. Deren Namen können im Prinzip beliebig gewählt werden, aber ihre Reihenfolge ist wichtig: Ganz links steht der Achsenabschnitt, auf den dann die Steigung folgt. Auf der rechten Seite des =|=Zeichens sind dann die Messwerte platziert, deren zeitlicher Abstand wiederum bestimmt, auf welche Werte die Pfadkoeffizienten fixiert werden. Anders als in Stata ist es nicht notwendig, die Pfade zwischen Achsenabschnitt und Messwerten auf den Wert 1 zu fixieren. Dies geschieht in MPlus per Voreinstellung, weil die Spezifikation vom Programm als Wachstumsmodell erkannt wird.
Data:
File is interesse-panel.dat ;
Variable:
Names are
int1 int2 int3 int4 int5 tn1 tn2 tn3 tn4 tn5;
Missing are all (-9999) ;
Usevariables are
int1 int2 int3 int4 int5;
Model: I S | int1@0 int2@14 int3@28 int4@46 int5@60