Dimensionen der Einstellungen zu Migranten
Seit dem Zweiten Weltkrieg sind fast alle westeuropäischen Gesellschaften zum Ziel von Migranten geworden, die selbst nicht aus westeuropäischen Ländern stammen. Die einheimischen Bevölkerungen reagieren auf dieses Phänomen häufig mit Ablehnung und Ängsten. Unter den Ängsten lassen sich idealtypisch zwei Dimensionen unterscheiden: Von primär sozio-ökonomische Befürchtungen bezüglich einer verschärften Konkurrenz um Arbeitsplätze und Sozialleistungen kann man Gefühle einer Bedrohung der eigenen Lebenswelt durch die fremden Kulturen abgrenzen.
Auch wenn diese Unterscheidung auf den ersten Blick plausibel erscheint, so stellt sich doch die Frage, ob Bedrohungsgefühle in der Praxis tatsächlich diese zweidimensionale Struktur aufweisen. Denkbar wäre beispielsweise auch, dass sich die Ablehnung der Migranten auf alle Lebensbereiche bezieht.
Mit Hilfe der ersten Welle des ESS lässt sich diese Frage empirisch prüfen. Der Fragebogen dieser Welle enthält u.a. zwei Items, die sozio-ökonomische Bedrohungsgefühle erfassen:
- “Was würden Sie sagen, nehmen Zuwanderer, die hierher kommen, im Allgemeinen Arbeitnehmern in Deutschland die Arbeitsplätze weg oder helfen sie im Allgemeinen, neue Arbeitsplätze zu schaffen?” (nehmen Arbeitsplätze weg (10) – schaffen neue Arbeitsplätze (0), imtcjob)
- “Die meisten Zuwanderer, die hierher kommen, arbeiten und zahlen Steuern. Sie nehmen außerdem das Gesundheitssystem und Sozialleistungen in Anspruch. Wenn Sie abwägen, denken Sie, dass Zuwanderer mehr bekommen als sie geben, oder mehr geben, als sie bekommen?” (bekommen mehr (10) – geben mehr (0) imbleco)
Zwei weiterer Items lassen sich der kulturellen Dimension zuordnen:
- “Würden Sie sagen, dass das kulturelle Leben in Deutschland im Allgemeinen durch Zuwanderer untergraben oder bereichert wird?” (untergraben (10) – bereichert (0) imueclt)
- “Wird Deutschland durch Zuwanderer zu einem schlechteren oder besseren Ort zum Leben?” (schlechterer Ort (10) – besserer Ort (0) imwbcnt)
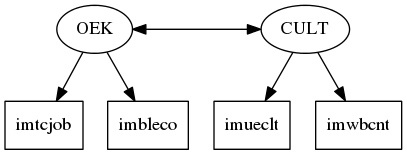
Figure 1: Zweidimensionales Modell
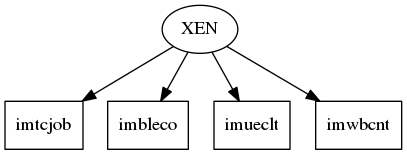
Alle vier Items sind so kodiert, dass hohe Werte für ablehnende, niedrige Werte hingegen für positive Einstellungen gegenüber Zuwanderern stehen. Die Abbildungen stellen die beiden alternativen Modelle graphisch dar. In der ersten Variante repräsentieren die beiden ersten Items eine ökonomische, die beiden anderen Items eine kulturelle Subdimension. Der Doppelpfeil zwischen den Faktoren repräsentiert eine vermutete Kovarianz zwischen beiden Unterdimensionen. In der zweiten Variante steht ein gemeinsamer Faktor hinter den vier Messungen.
Figure 2: Eindimensionales Modell
Welches Modell besser mit den Daten vereinbar ist, lässt sich ermitteln, indem die entsprechenden Strukturgleichungsmodelle geschätzt werden.
Konfirmatorische Faktorenanalyse in Stata
Der benötigte Datensatz läßt sich hier herunterladen, das untenstehende Syntaxfile hier.
Beide Modell-Varianten lassen sich dann sehr einfach in Stata implementieren:
use ess-w1-cfa, clear *bzw. use https://www.kai-arzheimer.com/beispiele-strukturgleichungsmodelle/ess-w1-cfa.dta, clear sem (imtcjob<-OEK) (imbleco<-OEK) (imueclt<-CULT) /// (imwbcnt<-CULT) , means(OEK@0 CULT@0) var(OEK@1 CULT@1) est store zweiml estat eqgof estat gof, stats(ic rmsea indices) sem (imtcjob<-XEN) (imbleco<-XEN) (imueclt<-XEN) /// (imwbcnt<-XEN) , means(XEN@0) var(XEN@1) est store einml estat eqgof estat gof, stats(ic rmsea indices)
Zunächst wird der Datensatz mit den vier Variablen eingelesen, dann wird das zweidimensionale Modell spezifiziert. Mit dem Pfeil-Symbol werden die Items imtcjob und imbleco als Indikatoren für latente ökonomische Bedrohungsgefühle definiert. Analog dazu werden die Items imueclt und imwbcnt als Indikatoren für kulturelle Bedrohungsgefühle festgelegt. Jede dieser Zuweisungen ist in ein Klammerpaar eingeschlossen. Variablen, die mit einem Großbuchstaben beginnen, werden als latente Variablen betrachtet. Abgetrennt durch ein Komma folgen dann die Optionen: means und var legen die Metrik, Mittelwerte Varianzen der latenten Variablen fest ( ). Hinter dem “at”-Zeichen (@) steht dabei der gewünschte Wert.
Wichtig ist, dass wie bei jedem Kommando in Stata die vollständige Modellspezifikation in einer einzigen Zeile stehen muss. Da dies schnell unübersichtlich werden kann, besteht die Möglichkeit, das Zeilenende durch drei Schrägstriche zu maskieren und die Eingabe in der nächsten Zeile fortzusetzen. Nach dem Absetzen dieses Kommandos werden die Modellschätzungen ausgegeben, die dann mit est store unter einem frei wählbaren Namen gespeichert werden können.
| imtcjob | OEK& | 1.321 | & | (0.0522) |
| imtcjob | Konstante& | 4.372 | & | (0.0472) |
| imbleco | OEK& | 1.296 | & | (0.0542) |
| imbleco | Konstante& | 4.019 | & | (0.0496) |
| imueclt | CULT& | 1.603 | & | (0.0556) |
| imueclt | Konstante& | 6.308 | & | (0.0548) |
| imwbcnt | CULT& | 1.809 | & | (0.0532) |
| imwbcnt | Konstante& | 4.997 | & | (0.0521) |
| cov(OEK,CULT)& | 0.826 | (0.0239) |
Die Tabelle zeigt die wichtigsten Ergebnisse dieser ersten Schätzung. Für jeden der vier Indikatoren ist jeweils ein Pfadkoeffizient, eine Faktorladung ausgewiesen, der wie ein Regressionskoeffizient zu interpretieren ist: Bei einer Zunahme der latenten Variable “ökonomische Bedrohungsgefühle” um eine Standardabweichung ist beispielsweise mit einer Zunahme der Zustimmung zum Arbeitsplätze-Item imtcjob um Skalenpunkte zu rechnen.
Darüber hinaus enthält für jedes Item den Effekt einer Konstanten, einen Achsenabschnitt. Dieser entspricht dem erwarteten Wert des jeweiligen Indikators, wenn der Wert der latenten Variablen bei ihrem Mittelwert von 0 liegt. Bei diesem einfachen Modell entsprechen die Achsenabschnitte dem jeweiligen empirischen Mittelwert der Items.
Stata nimmt per Voreinstellung Achsenabschnitte in das Modell auf, weil das Programm normalerweise Zugriff auf die Rohdaten hat. In älteren Programmen, die aus einer Zeit stammen, als primär Korrelations” und Kovarianzmatrizen analysiert wurden, die keine Informationen zur Höhe der Messwerte mehr enthalten, müssen die Achsenabschnitte teilweise explizit in das Modell aufgenommen werden.
Die letzte Zeile in schließlich enthält die Kovarianz zwischen beiden Faktoren. Da deren Metrik durch die var-Optionen standardisiert ist, reduziert sich die Kovarianz auf eine Korrelation und ist deshalb leicht zu interpretieren. Der vom Programm geschätzte Wert liegt mit recht hoch. Zwischen kulturellen und ökonomischen Bedrohungsgefühlen besteht also ein starker positiver Zusammenhang.
Die Ausgabe des zweiten sem-Befehls (hier nicht gezeigt) enthält die Faktorladungen der eindimensionalen Lösung, die insgesamt geringfügig niedriger ausfallen als bei der zweidimensionalen Lösung. Die Achsenabschnitte sind wiederum mit den empirischen Mittelwerten identisch.
| eindimensional | zweidimensional | |
|---|---|---|
| Parameter | 12 | 13 |
| 2 | 1 | |
| 63.9 | 12.8 | |
| RMSEA | .137 | .0843 |
| TLI | .897 | .961 |
| BIC | 26842 | 26799 |
| LL | -13377 | -13351 |
| N | 1659 | 1659 |
Die obenstehende Tabelle enthält Kriterien, anhand derer beide Spezifikationen verglichen werden können. Die zweidimensionale Lösung ist komplexer, da ein Parameter mehr geschätzt werden muß, erzielt aber auch eine deutlich bessere Anpassung an die Daten. Nach allen gängigen Kriterien ist ihr der Vorzug zu geben.
Konfirmatorische Faktorenanalyse in LISREL
Auch in LISREL läßt sich das Problem in sehr kompakter Form formulieren. Um dies nachvollziehen zu können, werden wiederum die Syntax-Datei sowie die Rohdaten benötigt.
Raw Data From File ess-w1-cfa.lsf Latent Variables: OEK CULT Relationships imtcjob = CONSTANT + OEK imbleco = CONSTANT + OEK imueclt = CONSTANT + CULT imwbcnt = CONSTANT + CULT End of Problem
Die erste Zeile lädt den Datensatz in einem binären Format, das hier als “roh” bezeichnet wird, da das Programm standardmäßig immer noch die Eingabe von Kovarianz- bzw. Korrelationsmatrizen erwartet. Anders als in Stata müssen dann die latenten Variablen explizit definiert werden. Das Schlüsselwort Relationships markiert dann den Beginn eines Blocks, der die Gleichungen des Messmodells enthält. Anders als in Stata steht jede Gleichung in einer eigenen Zeile. Außerdem ist es notwendig, den Achsenabschnitt mit dem Schlüsselwort CONSTANT explizit in die Gleichungen aufzunehmen. Die Metrik der latenten Variablen muss hingegen nicht explizit auf einen Mittelwert von 0 und eine Varianz von 1 festgelegt werden, da dies der Voreinstellung entspricht. Auch die Kovarianz Korrelation zwischen den Faktoren wird automatisch geschätzt. Die Schlüsselworte End of Problem markieren das Ende der Eingabe.
Konfirmatorische Faktorenanalyse in MPlus
Auch in MPlus läßt sich das Modell sehr einfach schätzen (Eingabe und Daten hier).
Data:
File is ess-w1-cfa-raw.dat ;
Variable:
Names are
imtcjob imbleco imueclt imwbcnt;
Missing are all (-9999) ;
Model:
OEK BY imtcjob* imbleco ;
OEK@1 ;
CULT BY imueclt* imwbcnt ;
CULT@1 ;
MPlus-Eingabeskripte bestehen aus mehreren Blöcken. Im ersten dieser Blöcke wird die Datenquelle benannt. MPlus akzeptiert nur Daten im Textformat. Rekodierungen und Transformationen sollten in einem anderen Statistikpaket vorgenommen werden. In Stata ist es mit Hilfe des benutzerdefinierten Kommandos stata2mplus 1 leicht möglich, die benötigten Variablen auszuwählen und in einer für lesbaren Datei zu speichern. stata2mplus erzeugt außerdem ein Programmfragment, das die Daten in einliest und um die Anweisungen für die eigentliche Modellierung ergänzt werden kann.
Im zweiten Block müssen die beobachteten Variablen deklariert werden, da die Textdatei mit den Messwerten keine Information über die Variablennamen oder die Interpretation bestimmter Werte als Indikator für missing values enthält. Im dritten Block wird dann das Modell definiert.
Die Struktur der Syntax unterscheidet sich dabei geringfügig von den entsprechenden Codeblöcken in Stata und LISREL. Während dort die Indikatoren durch ihre Beziehung zu den Faktoren definiert wurden, stehen die Namen der Faktoren hier zu Beginn der Zeilen, gefolgt von dem Schlüsselwort BY, das angibt, mit welchen Indikatoren die Faktoren gemessen werden.
Wichtig ist dabei der Stern, der an die Namen der jeweils ersten Indikatoren angehängt wird. Dieser bedeutet, dass der entsprechende Pfadkoeffizient frei geschätzt werden soll. Per Voreinstellung würden diese Pfadkoeffizienten ansonsten auf den Wert 1 gesetzt. In Kombination mit den Zeilen 9 und 11, in denen mit Hilfe des @-Zeichens die Varianz der Faktoren auf den Wert 1 gesetzt wird, wird so die Metrik der latenten Variablen definiert. Damit ist die Eingabe abgeschlossen.
Footnotes:
Mit ssc install stata2mplus kann das Kommando aus dem Internet installiert werden. Mit ssc install runmplus lässt sich ein weiterer benutzerdefinierter Befehl installieren, der das Zusammenspiel von und noch stärker automatisiert.