Was ist ein Strukturgleichungsmodell?
Ein Strukturgleichungsmodell (englisch: Structural Equation Model = SEM) beinhaltet ein System von Beziehungen zwischen beobachtbaren Variablen (Indikatoren oder manifeste Variablen) und nicht-beobachtbaren Variablen (Konstrukte, latente Variablen oder Faktoren). Nach dem ersten Programm zur Schätzung von Strukturgleichungsmodellen, das für normale Anwender handhabbar war, werden Strukturgleichungsmodelle manchmal auch als LISREL-Modelle bezeichnet. Weitere Programme, mit denen die Parameter eines Strukturgleichungsmodelles geschätzt werden können, sind MPlus, Amos, EQS, Stata und R.
Übersicht
Strukturgleichungsmodelle verbinden zwei wichtige Analyseverfahren: die Faktorenanalyse, mit der latente Variablen untersucht werden, und die Pfadanalyse, die Systeme mit mehreren abhängigen Variablen abbilden kann. Das macht sie für Sozialwissenschaftler attraktiv, denn unsere Theorien bestehen oft aus einem ganzen Netz von Annahmen über die Zusammenhänge zwischen Variablen, von denen viele nicht direkt beobachtbar sind. Ein Beispiel ist der vermutete Zusammenhang zwischen Deprivationserfahrungen, Fremdenfeindlichkeit und der Wahl rechter Parteien. Die Strukturgleichungsmodellierung hat sich deshalb in den letzten Jahren zu einem Standardverfahren der Empirischen Sozialforschung entwickelt.
Die wichtigsten Annahmen, Grundbegriffe und Anwendungsmöglichkeiten zum Thema erkläre ich in meiner Vorlesung:

Was kann ich mit einem Strukturgleichungsmodell anfangen?
In der Politischen Soziologie, der Sozialpsychologie und der Politikwissenschaft sind Strukturgleichungsmodelle oft das Mittel der Wahl, weil mit ihrer Hilfe komplexe Zusammenhänge zwischen beobachteten und nicht beobachteten Variablen analysiert werden können. Ein Beispiel dafür ist der Aufsatz “Christian Religiosity and Voting for West European Radical Right Parties” (Arzheimer/Carter 2009) (“Christian Religiosity & the Radical Right” hier auch als frei zugänglicher pre-print). In diesem Beitrag prüfen wir drei Hypothesen:
- Vor allem in der US-amerikanischen Forschung zeigt sich seit Jahrzehnten, dass sehr fromme Menschen gegenüber Andersgläubigen und ethnischen Minderheiten sehr negative Einstellungen entwickeln.
- Zugleich propagiert das Christentum Toleranz, Mitgefühl und Nächstenliebe. Deshalb wäre zu erwarten, dass gläubige Christen benachteiligten Minderheiten positiv gegenüber stehen.
- Vor allem im europäischen Kontext ist außerdem zu erwarten, dass überzeugte Christen eine Parteibindung zu einer konservativen oder christdemokratischen Partei entwickeln und deshalb für die Radikale Rechte nicht verfügbar sind.
Alle drei Hypothesen können wir mit einem (komplexen) Strukturgleichungsmodell testen. Die latente Variable “christliche Religiosität” messen wir mit vier Indikatoren; die latente Variable “radikale rechte Einstellungen” sogar mit mehr als zehn Indikatoren. Wir gehen außerdem davon aus, dass eine Korrelation zwischen Parteibindung und rechten Einstellungen besteht, dass alle Einstellungsvariablen in einem Zusammenhang mit soziodemographischen Merkmalen wie Alter, Geschlecht und Bildung stehen, und dass sowohl die Einstellungs- als auch die soziodemographischen Variablen einen Effekt auf das Wahlverhalten haben. Das Ergebnis sieht so aus:
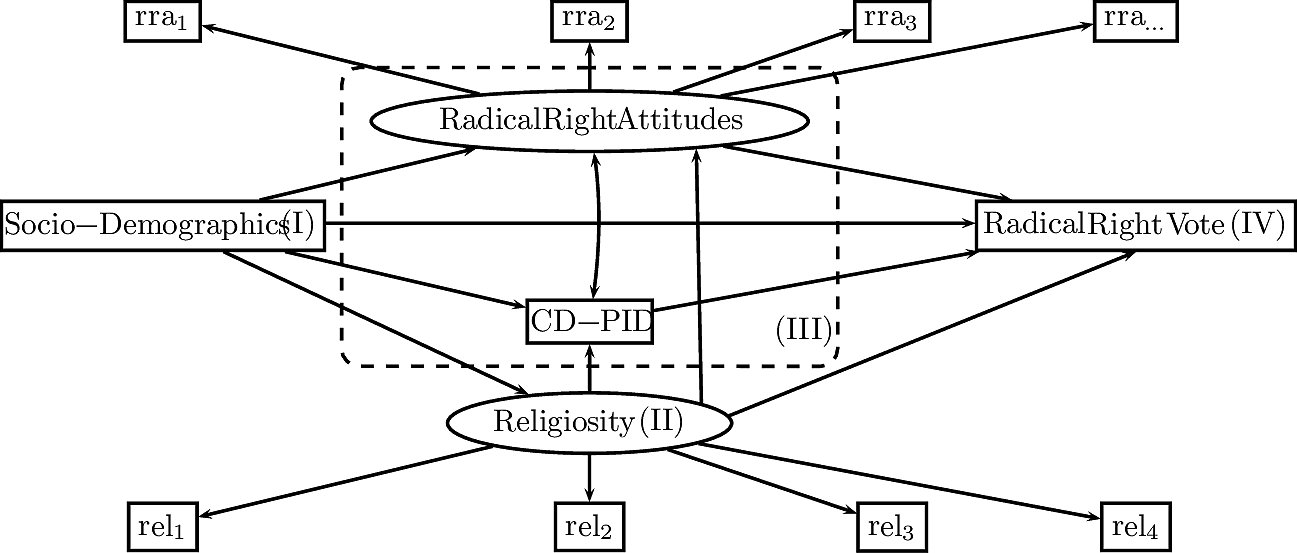
Eine Besonderheit unseres Modells besteht darin, dass sowohl die manifeste abhängige Variable (Wahl einer radikalen Rechtspartei) als auch eine der latenten Variablen (Identifikation mit einer christdemokratischen oder konservativen Partei) dichotom sind, also nur die Werte 0 oder 1 annehmen können. Moderne Programme können auch mit nicht-kontinuierlichen Variablen umgehen.
Kann man mit Strukturgleichungsmodellen Kausalität prüfen?
In der Literatur werden Strukturgleichungsmodelle manchmal auch als Kausalmodelle bezeichnet. Deshalb gehen viele Anwender davon aus, dass man mit einem Strukturgleichungsmodell das Vorliegen von Ursache-Wirkungs-Zusammenhängen testen kann. Leider stimmt dies so nicht. Der Beiname “Kausalmodell” erklärt sich daraus, dass im Strukturgleichungsmodell solche Annahmen explizit ausformuliert werden. In welche Richtung die Kausalität wirkt, lässt sich mit einem Strukturgleichungsmodell aber per se genauso wenig entscheiden wie mit einem normalen Regressionsmodell. Entscheidend ist hier vielmehr das Forschungsdesign, mit dem die Daten erhoben wurden:

Manchmal lassen sich aber auf Grund logischer Überlegungen zumindest Gruppen von Variablen bilden, die in einer eindeutigen kausalen Reihenfolge stehen müssen. Im Beispiel sieht das so aus:

Lehrbuch Strukturgleichungsmodelle für Politikwissenschaftler
Wer mehr zum Thema Strukturgleichungsmodell erfahren möchte, kommt aber um die Lektüre eines Lehrbuches nicht herum. Für den englischsprachigen Markt existiert seit langem eine ganze Reihe hervorragender Lehrwerke, und mit dem Buch von Jost Reinecke ist vor einigen Jahren eine gute deutschsprachige Ergänzung zu diesen hinzugekommen. Bislang fehlt es aber an einer anwendungsorientierten Einführung für Politikwissenschaftlerinnen und Politikwissenschaftler. Ziel meines Lehrbuches (das natürlich auch für andere Sozialwissenschaftlerinnen und Sozialwissenschaftler geeignet ist) ist es, diese Lücke zu schließen.
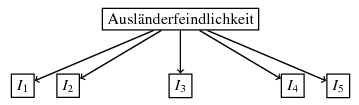
Vorgestellt werden grundlegende Modelle zur Messung politikwissenschaftlicher Konstrukte (z.B. Fremdenfeindlichkeit und political efficacy), zur Schätzung von Messfehlern und zur Modellierung von Beziehungen zwischen latenten Variablen. Als fortgeschrittene Themen werden u.a. latente Wachstumsmodelle und fehlende Werte (missing values) behandelt. Der Schwerpunkt liegt dabei auf der Illustration durch politikwissenschaftliche Beispiele, die durch Hinweise zur Umsetzung der Verfahren in Standardprogrammen (LISREL, Stata, MPlus) ergänzt werden. Als Leseprobe können das Inhaltsverzeichnis, die Einleitung und das Glossar heruntergeladen werden. Weitere Lesproben gibt es bei Google Books, bei Amazon und beim Verlag.
Der Inhalt im einzelnen:
Strukturgleichungsmodell: Beispiele
Im Mittelpunkt des Buches stehen die wichtigsten politikwissenschaftlichen Anwendungsfälle für den Einsatz von Strukturgleichungsmodellen. Dazu gehört vor allem die konfirmatorische Faktorenanalyse (Schätzung eines Modells zur Messung latenter Variablen), die am Beispiel der Einstellungen zu Migranten vorgestellt wird. Zu den wichtigsten Komplikationen der konfirmatorischen Faktorenanalyse zählen der Gruppenvergleich und die vorgelagerte Frage nach der Äquivalenz von Messungen über kulturelle, Sprach- und Ländergrenzen hinweg. An Beispielen aus der Praxis zeigt das Buch, wie diese Fragen mit den gängigen Programmen zur Analyse von Strukturgleichungsmodellen untersucht werden können. Ebenfalls ausführlich vorgestellt wird der Umgang mit kategorialen Variablen, die in politikwissenschaftlichen Anwendungsfällen eher die Regel als die Ausnahme darstellen. Zuletzt schließlich werden latente Wachstumsmodelle präsentiert, die die Veränderung einer latenten Variablen über die Zeit beschreiben. Den vollständigen Quellcode und die Datensätze für alle Beispiele aus dem Buch (Daten und Code für Stata, LISREL, MPlus) gibt es hier zum Download.
Der Inhalt im Überblick:
Einleitung
Das Einleitungskapitel stellt die Grundzüge der beiden Verfahren vor, auf denen die Modellierung von Strukturgleichungsmodellen basiert: die Pfadanalyse und die Faktoranalyse. Es gibt außerdem einen Überblick über den Aufbau des Buches, die einschlägige Software und die wichtigsten Internetquellen.
Strukturgleichungsmodelle: Grundlagen
Das zweite Kapitel ist den Grundlagen des Verfahrens gewidmet und ist vor allem zum späteren Nachschlagen gedacht. Zu diesen Grundlagen gehören zum einen eine knappe Einführung in die Matrixalgebra, zum anderen ein zweiter Blick auf die Bausteine des Modells: Korrelationsrechnung, Regressionsrechnung, Faktorenanalyse und die Grundzüge der klassischen Testheorie. Im Anschluss daran werden das allgemeine Strukturgleichungsmodell vorgestellt und wichtige Grundfragen der Modellierung (u.a. Schätzverfahren und Identifikation von Modellen) erörtert.
Strukturgleichungsmodelle: Beispiele und Anwendungen
Für Politikwissenschaftler ist der wichtigste Anwendungsfall der Strukturgleichungsmodellierung die Schätzung konfirmatorischer Faktorenanalyse. In diesem Kapitel wird an vielen ausführlich kommentierten Beispielen und mit realen Daten (European Social Survey, ALLBUS) gezeigt, wie sich solche Modelle mit Hilfe der gängigen Programme schätzen lassen.
Strukturgleichungsmodelle: Fortgeschrittene Themen und Ausblick
Zu den fortgeschritten Themen, die für Politikwissenschaftler relevant sind, gehört vor allem der Umgang mit kategorialen Variablen, der wiederum mit einem Beispiel aus der politikwissenschaftlichen Einstellungsforschung illustriert wird. Relativ neu für die Politikwissenschaft sind die latenten Wachstumsmodelle, die die Veränderung einer Variablen über die Zeit beschreiben. Eine solche Variable ist das Interesse am Wahlkampf, das im Lauf der Kampagne mehr oder minder stark zunimmt. Weitere fortgeschrittene Themen, die in diesem Kapitel in knapperer Form vorgestellt werden, sind missing data, kategoriale latente Variablen und Mehr-Ebenen-Strukturgleichungsmodelle.